we need some assumptions before solving this question:
- negligible kinetic energy
- no pressure changes
- no shaft work
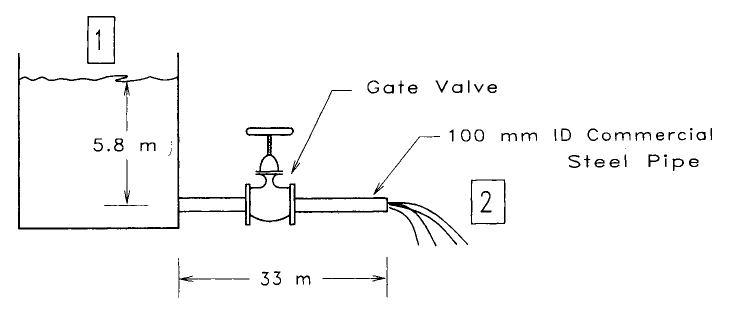
applying mechanical energy balance between point 1 and point 2 we get
$$\frac g{g_c}\bigtriangleup z+F=0$$
for water
$$µ=1.0\times10^{-3}kg/ms$$
$$\rho=1000kg/m^3$$
For pipe entrance K factor ,
$$K_f=\frac{160}{Re}+0.50$$
For gate valve,
$$K_f=\frac{300}{Re}+0.10$$
For pipe exit,
$$K_f=1.0$$
for pipe length,
$$K_f=\frac{4fL}d=\frac{4f\times33}{0.10}=1320f$$
adding all K factors we get
$$\sum K_f=\frac{460}{Re}+1320f+1.60$$
for Re>10,000
$$\sum K_f\approx1320f+1.60$$
followed by
$$F=\sum K_f\left(\frac{u^{-2}}{2g_c}\right)=(660f+0.80)ū^2$$
gravitation energy is given by
$$\frac g{g_c}\triangle z=\left(\frac{9.8m/s^2}{1kg\;m/s^2/N}\right)\left(0-5.8m\right)=-56.8Nm/kg=-56.8J/kg$$
because of our assumptions mechanical energy balance becomes,
$$\frac{{ū^2}_2}{2g_c}+\frac g{g_c}\triangle z+F=0$$
Solving for the exit velocity and substituting for the height change gives
$${ū^2}_2=-2g_c\left(\frac g{g_c}\triangle z+F\right)=-2g_c\left(-56.8+F\right)$$
reynolds number is given by
$$Re=\frac{dū\rho}\mu=\frac{0.1\times ū\times1000}{1.0\times10^{-3}}=1.0\times10^5ū$$
for commercial steel pipe, ε=0.0046mm
$$\frac\varepsilon d=\frac{0.0046mm}{100mm}=0.00046$$
Through trial and error we make the following table
| Guessed ū (m/s) | Re | f | F | Calculated ū (m/s) |
| 3 | 300,000 | 0.00451 | 34.09 | 6.75 |
| 3.50 | 350,000 | 0.00446 | 46 | 4.66 |
| 3.66 | 366,000 | 0.00444 | 50.18 | 3.66 |
thus velocity of liquid discharging from the pipe is 3.66 m/s
for finding value of F for fully developed turbulent flow in rough pipes we use
$$\frac1{\sqrt[{}]f}=4\log\left(3.7\frac d\varepsilon\right)$$
we get approximately value $$3.51{ū^2}_2$$
therefore
$$F=\left(660f+0.80\right){ū^2}_2=3.51{ū^2}_2$$
on solving we get
$$ū_2=3.76\;m/s$$
which is close to our trial and error table solution
cross-sectional area of pipe is
$$A=\frac{\mathrm{πd}^2}4=\frac{3.14\times0.1}4=0.00785\;m^2$$
mass flow rate is given as
$$Q_m=\rho ūA=1000\times3.66\times0.00785=28.8\;kg/s$$